KMP 算法
1. 暴力匹配
本文中 txt 表示原字符串 pat 表示需要匹配的子串
int search(String pat, String txt) {
int M = pat.length();
int N = txt.length();
for (int i = 0; i <= N - M; i++) {
int j;
for (j = 0; j < M; j++) {
if (pat[j] != txt[i+j])
break;
}
// pat 全都匹配了
if (j == M) return i;
}
// txt 中不存在 pat 子串
return -1;
}

2. 自动转换机匹配算法
KMP 通过构建 dfa 来匹配字符串,只有达到最终状态才算匹配.两个变量 i:遍历数组 j: 表示当前状态
dfa 通过当前输入的字符来处理当前状态移动.
数组 dfa[state][char] = nextstate
dp[4]['A'] = 3 表示:
当前是状态 4,如果遇到字符 A,
pat 应该转移到状态 3
因此写出搜索函数
int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
// 如果达到终止态,返回匹配开头的索引
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
下面重点如何构造出 dfa :
int M = needle.size();
int** dfa = new int*[M];
for(int i = 0;i<M;i++)
{
dfa[i] = new int[26]; // 构造 dfa
}
for(int i = 0;i<M;i++)
{
for(int j = 0;j<26;j++)
dfa[i][j] = 0;
}
dfa[0][needle[0] - 'a'] = 1;
int X = 0;
for(int j = 1;j<M;j++)
{
for(int c = 0;c < 26;c++)
{
if( (int)(needle[j]-'a') == c)
dfa[j][c] = j+1;
else
dfa[j][c] = dfa[X][c];
}
X = dfa[X][needle[j] - 'a'];
}
3. KPM
3.1 匹配过程
优化朴素算法,比如在模式串的第六个位置匹配失败我们其实是知道当前主串S前五位字符的信息的,因此我们可以
修改 j 来优化下一次开始匹配的位置。
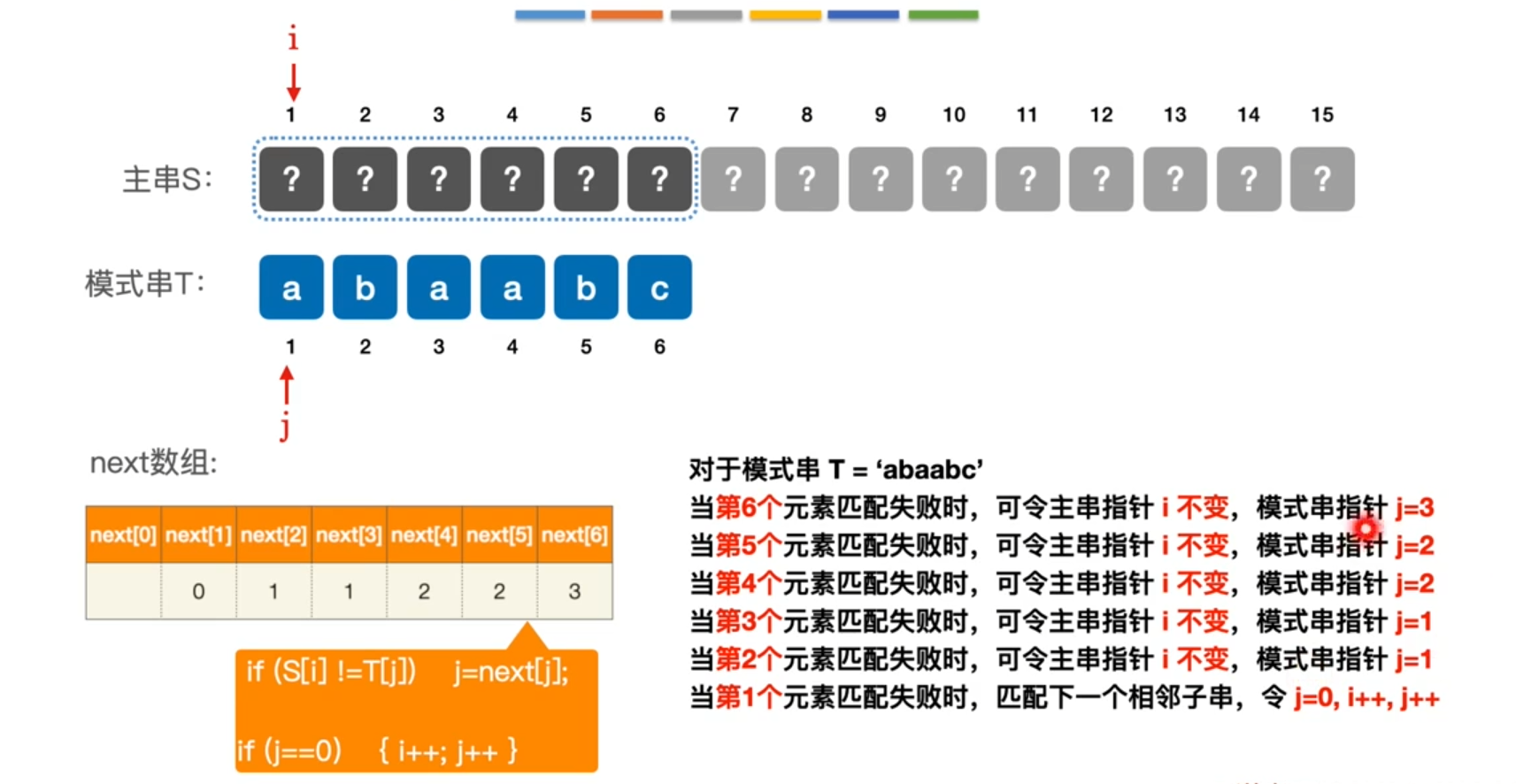
例如在 i = 6 处匹配失败此时得到前五位信息,经过之前的信息优化只需要到 j = 3 处进行下一次匹配
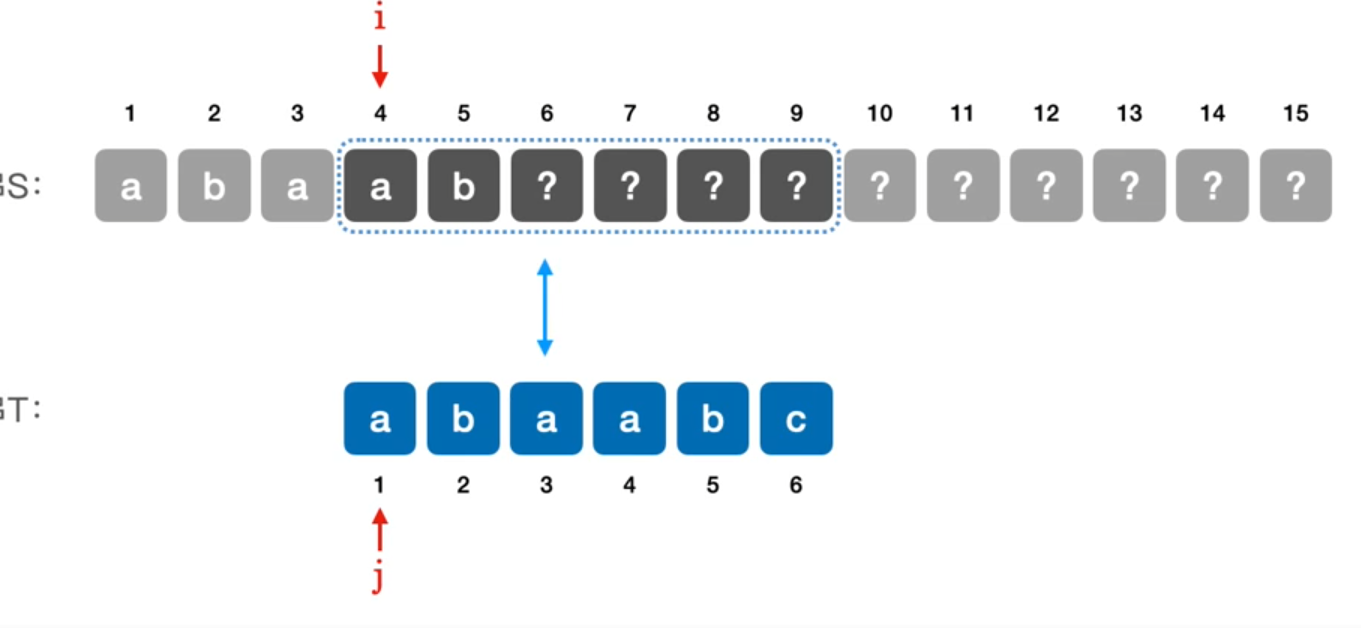
for(int i = 0;i < S.size;) // 注意 i 在下方控制
{
if(S[i] != T[j]) j = next[j];
if(j == 0) {j++;i++;}
}
因此 KMP 需要对模式串进行预处理得到 next[] 再进行匹配


上面表示的都是下标 1 开始的情况
最坏时间复杂度 O(n+m)
3.2 求解 next
int GetNext(string s,int next[])
{
next[0] = -1;
int i = 0, j = -1;
while(i < s.size())
{
if(j==-1 || ch[i] == ch[j]) next[++i] = ++j;
else j = next[j];
}
}
前缀: 包含首位但不包含末尾
后缀:包含末位字符但不包含首位字符的子串。
next[j]: KMP 算法和核心就是匹配失败后将模式串的公共前缀移动到公共后缀上,此时 next 将会指向下一次需要和模式串比较的地方,因此计算此值其值第 j 位字符前面 j-1位字符组成的子串的前后缀重合字符数 +1 (手算方式,这里的 +1 是因为编号从 1 开始了)
求解next数组其实本质就是一个递归比较
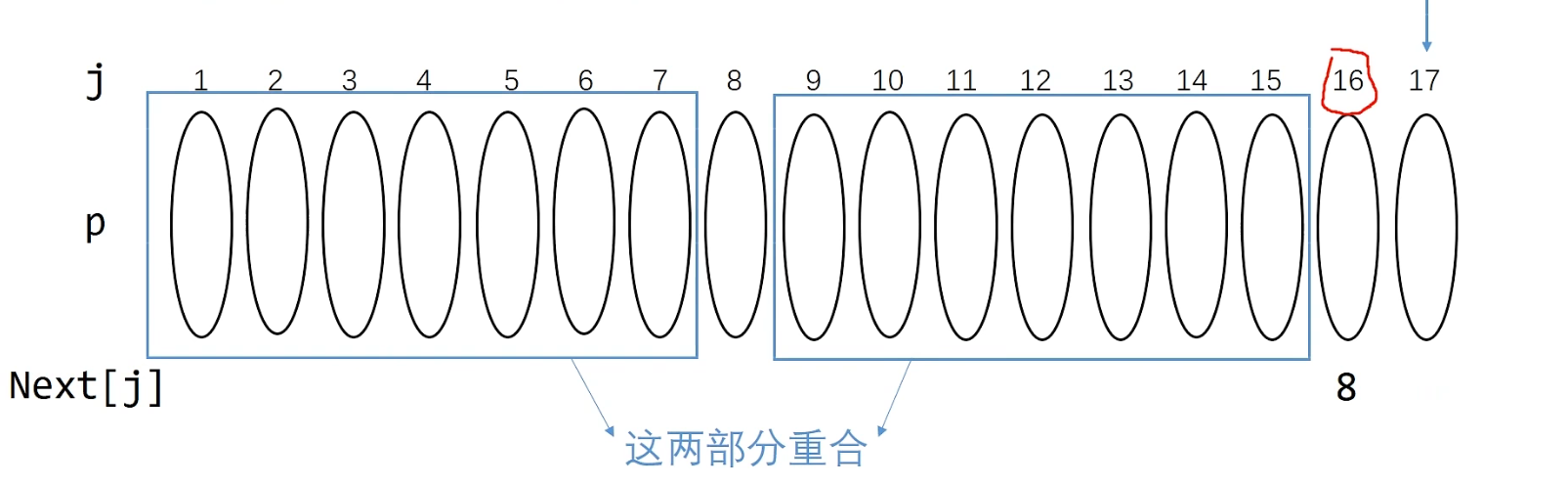
假设 next[16] = j = 8 当前求 next[17],自然得到两种情况
- 当 s[16] == s[8] 时得到当前后缀最大重合 8 位,得到s[17] == 8+1;
- 如果不相等就需要 j 往前看即得到 j = next[j];
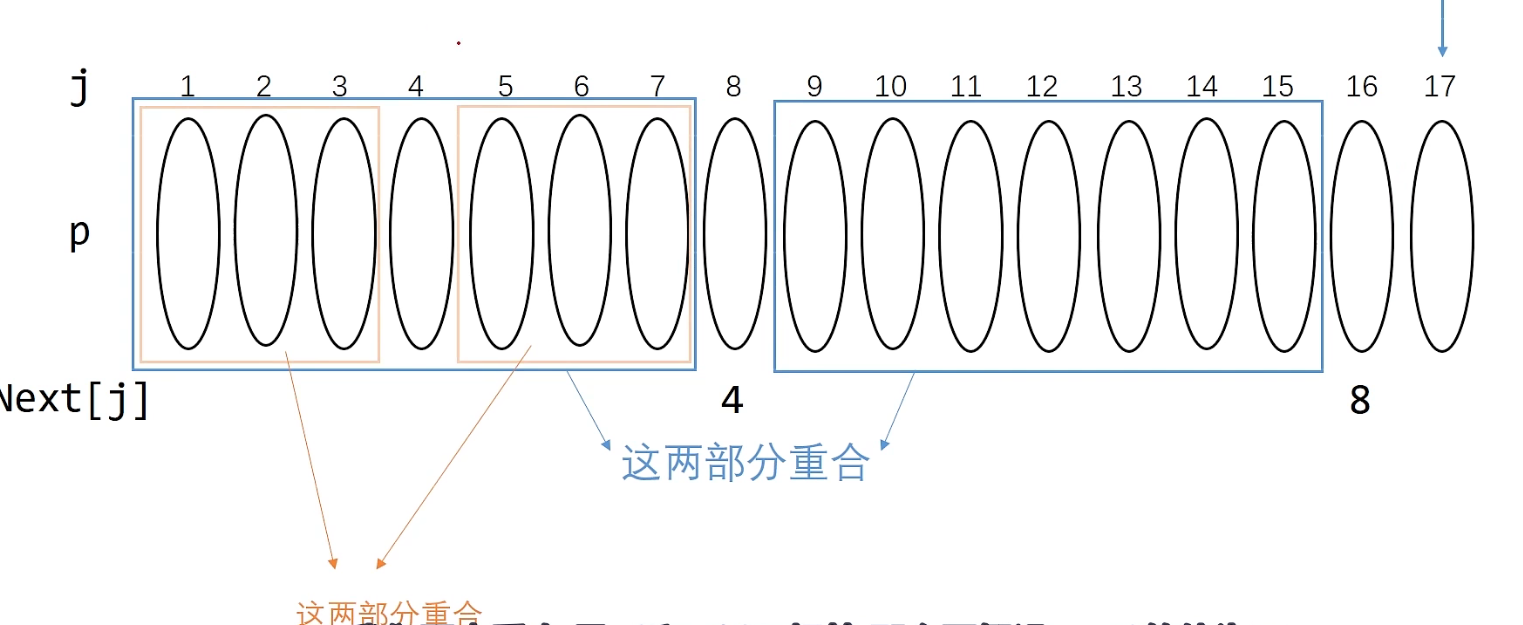
假设 next[8] = 4 证明三位最大前后缀相等,那么当前就需要判断 s[4] 和 s[16] 同样是两种情况
- 如果相等证明此时前16位最大前后缀是4,自然得到 next[17] = 4+1;
- 如果不相等继续往前找 如此递归最终得到一个线性复杂度O(n) getNext
可以简单记忆成看门牌求解,当前求的是 next[i+1] 那么去看 i 的门牌假设是 j,比较的是 a[i]=a[j],如果相等直接返回到 a[i+1] = j+1;
3.3 实际代码
int strStr(string s, string pat) {
int next[1000] = {0};
int j = -1;
int i = 0;
next[0] = -1;
while(i < pat.size() -1)
{
if(j == -1 || pat[i] == pat[j]) next[++i] = ++j;
else j = next[j];
}
i = 0; j = 0;
while(i < s.size())
{
if(j == -1 || s[i] == pat[j])
{
++i;++j;
}
else
{
j = next[j];
}
if(j == pat.size())
{
return i - pat.size();
}
}
return -1;
}
3.4 进一步优化
找 next[j] 的指向位,比如 next[j]=3 找 A[3] ?= A[j] 如果相等把 nextval[j] = nextval[3];